温馨提示:本文含有很多公式,若格式没有加载出来,请刷新页面
0/1背包问题:n种物品和一个背包,物品i的重量是wi,其价值为vi,背包的容量为C。背包问题是如何选择装入背包的物品,使得装入背包中物品的总价值最大?如果在选择装入背包的物品时,对每种物品i只有两种选择:装入背包或不装入背包,即不能将物品i装入背包多次,也不能只装入物品i的一部分
有5个物品,其重量分别是{2, 2, 6, 5, 4},价值分别为{6, 3, 5, 4, 6},背包的容量为10
1.动态规划法
0/1背包问题可以看作是决策一个序列(x_1, x_2, …, x_n),对任一变量x_i的决策是决定x_i=1还是x_i=0。设V(n, W)表示将n个物品装入容量为W的背包获得的最大价值,
显然,初始子问题是把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包,得到的价值均为0,即:V(i, 0)= V(0, j)=0\ \ \ (0≤i≤n, 0≤j≤W)
考虑原问题的一部分,设V(i, j)表示将前i(1≤i≤n)个物品装入容量为j(1≤j≤W)的背包获得的最大价值,则有求解子决策x_i时的递推式:
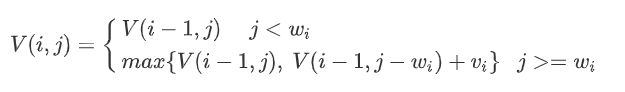
为了确定装入背包的具体物品,从最后一个值向前推,如果V(n,W)>V(n-1,W),表明第n个物品被装入背包,前n-1个物品被装入容量为W-w_n的背包中;否则,第n个物品没有被装入背包,前n-1个物品被装入容量为C的背包中。依此类推,直到确定第1个物品是否被装入背包中为止。由此,得到如下函数:
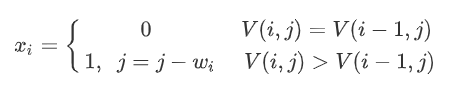
重抄一下题目:有5个物品
x_1,x_2,x_3,x_3,x_4,x_5其重量分别是w_i=\{2, 2, 6, 5, 4\},价值分别为v_i=\{6, 3, 5, 4, 6\},背包的容量$W=10$
解题过程为:
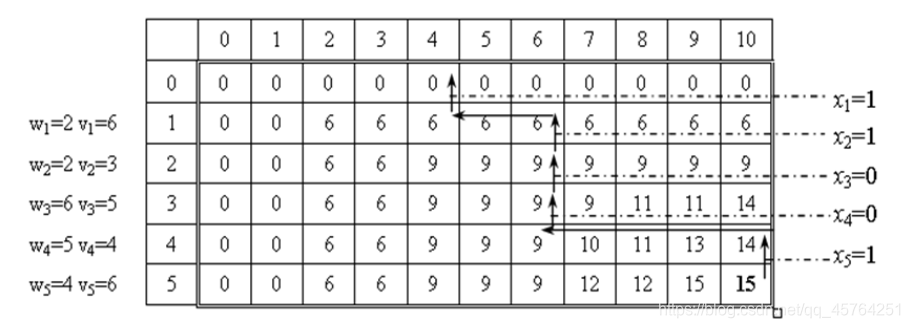
重点就是构造出如下表格,列 i 表示这5个物品,行 j 表示背包容量,每一格里就是目前背包内价值
-
每个格子的值就是V(i,j),依据上面的表达式依次填表如下:
比如:求(1,2)格的值,
j=2=w_1=2,所以V(1,2)=max{V(0,2),V(0,2-2=0)+6}=max{0,6}=6 -
逆序依照第二个函数表达式求解每个物品
x_i是0还是1,1代表装入,0则不装比如:求
x_5,则i=5,j=10,因为V(5,10)=15>V(4,15)=14,所以为1,且j=10-4=6;再求x_4,i=4,j=6,同理…….则得出第1、2、5个物品装入时,价值最大。
2.分支限界法
一般情况下,假设当前已对前i个物品进行了某种特定的选择,且背包中已装入物品的重量是w,获得的价值是v,计算该结点的目标函数上界的一个简单方法是,将背包中剩余容量全部装入第i+1个物品,并可以将背包装满,于是,得到限界函数:
ub=\ v_i+(W-w_i)\times (V_{i+1}/W_{i+1})
(理解:背包剩余空间放入价值重量比(v/w)最大的物品)
依上计算从根结点到叶子结点的目标函数值直到表PT中取得极大值。
重抄一下题目:有5个物品
x_1,x_2,x_3,x_3,x_4,x_5其重量分别是w_i=\{2, 2, 6, 5, 4\},价值分别为v_i=\{6, 3, 5, 4, 6\},背包的容量W=10
x1 x2 x3 x4 x5 重量w 2 2 6 5 4 价值v 6 3 5 4 6 价值重量比V/W 3 1.5 0.83 0.8 1.5
按价值重量比从大到小:x1、x2、x5、x3、x4
算法步骤:
-
根据限界函数计算目标函数的上界16.67;采用贪心法得到下界12;
*(上界:按重量比从大到小放进去,x1、x2、x5都可以,直到x3时,背包剩余容量2、总价值为15,若将背包填满,则将x3放入重量为2即1/3,此时背包内总价值为15+51/3=16.67;下界:每次放入价值最大的,直至放不进去,即6+6=12)**
-
计算根结点的目标函数值并加入待处理结点表PT;
-
循环直到某个叶子结点的目标函数值在表PT中取极大值
3.1 i = 表PT中具有最大值的结点;
3.2 对结点i的每个孩子结点x执行下列操作:
3.2.1 如果结点x不满足约束条件,则丢弃该结点;
3.2.2 否则,估算结点x的目标函数值lb,将结点x加入表PT中; -
将叶子结点对应的最优值输出,回溯求得最优解的各个分量;
题解二叉树:
(对每一个物品进行求值比较,在界限内取最大的一条路。左为1,即放入,此时,必须装上这个物品,其他的同样计算;右为0,此时,出去这个物品,对剩余物品同样计算。
比如:
x1=1时,背包剩余容量8,已有价值6,剩余价值重量比排序x2、x5、x3、x4,再放入x2、x5和x3的1/3,ub=16.67;
x1=0时,背包剩余容量10,已有价值0,剩余价值重量比排序x2、x5、x3、x4,再放入x2、x5和x3的2/3,ub=12.33)
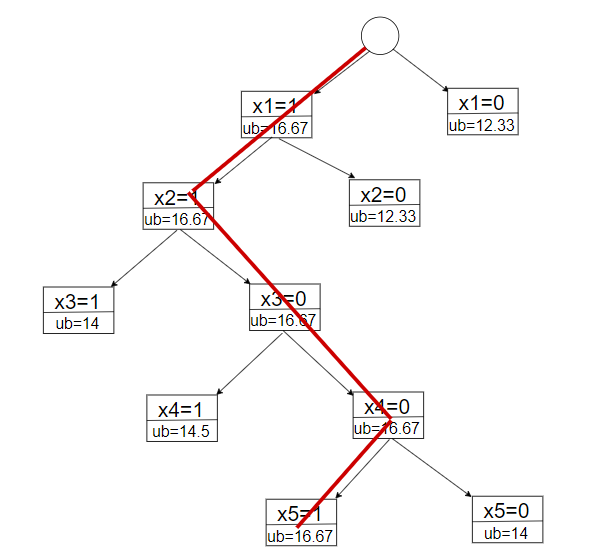
注:这种解法中,重量价值比也称为性价比
3.回溯法
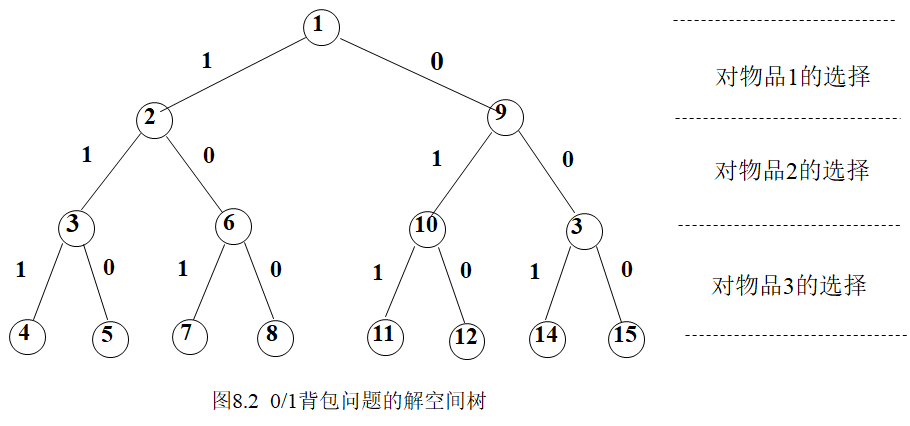
对于0/1背包问题,回溯法最后构造的是纵向的子集树,如下是n=3时的解空间树,解的个数是2^n,n是物品个数
重抄一下题目:有5个物品
x_1,x_2,x_3,x_3,x_4,x_5其重量分别是w_i=\{2, 2, 6, 5, 4\},价值分别为v_i=\{6, 3, 5, 4, 6\},背包的容量W=10
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| 重量w | 2 | 2 | 6 | 5 | 4 |
| 价值v | 6 | 3 | 5 | 4 | 6 |
由上面表格可以看的更直观,最终画的解空间树如下,即是一个个地让物品放进去,看结果。
每个物品两个状态,放进去为1,不放进去为0。
超重即为走不通的情况,图上表现为\times,则回溯到有兄弟结点可以走的父节点,走兄弟节点这一种情况。
最后得到各种情况的解(总价值),再比较一下即可得到最优解。